Stack

스택

 

스택(stack)의 특성

• 물건을 쌓아 올리듯 자료를 쌓아 올린 형태의 자료구조
• 스택에 저장된 자료는 선형 구조를 갖는다. 
  • 선형구조 : 자료 간의 관계가 1대 1의 관계를 갖는다.
  • 비선형구조 : 자료 간의 관계가 1대 N의 관계를 갖는다. (예: 트리)
• 스택에 자료를 삽입하거나 스택에서 자료를 꺼낼 수 있다.
• 마지막에 삽입한 자료를 가장 먼저 꺼낸다.
  • 후입 선출(LIFO, Last-in-first-out) 이라고 부른다.
  • ex) 스택에 1,2,3 순으로 자료를 삽입한 후 꺼내면 역순 - 3,2,1 순으로 꺼낼 수 있다.

 

스택의 구현

스택을 프로그램에서 구현하기 위해서 필요한 자료구조와 연산

• 자료구조: 자료를 선형으로 저장할 저장소
  • 배열을 사용할 수 있다.
  • 저장소 자체를 스택이라 부르기도 한다.
  • 스택에서 마지막 삽입된 원소의 위치를 top이라 부른다.
• 연산
  • 삽입 : 저장소에 자료를 저장한다. 보통 push 라고 부른다.
  • 삭제 : 저장소에서 자료를 꺼낸다. 꺼낸 자료는 삽입한 자료의 역순으로 꺼낸다. 보통 pop이라고 부른다.
  • 스택이 공백인지 아닌지를 확인하는 연산 .isEmpty
  • 스택의 top에 있는 item(원소)을 반환하는 연산 .peek

 

스택의 삽입 / 삭제 과정

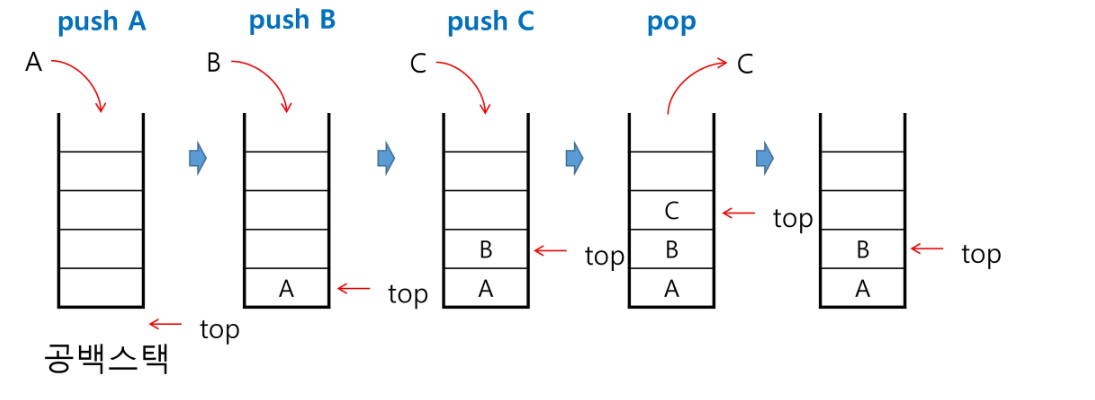
• 빈 스택에 원소 A,B,C를 차례로 삽입 후 한번 삭제하는 연산과정

 

스택의 push 알고리즘

• append 메소드를 통해 리스트의 마지막에 데이터를 삽입

def push(item):
    s.append(item)

def push(item, size):
    global top
    top += 1
    if top == size:
        print('overflow!')
    else:
        stack[top] = item


size = 10
stack = [0] * size
top = -1

push(10, size)
top += 1  # push(20)
stack[top] = 20

 

스택의 pop 알고리즘

 

def pop():
    if len(s) == 0:
        # underflow
        return
    else:
        return s.pop()

def pop():
    global top
    if top == -1:
        print('underflow')
        return 0
    else:
        top -= 1
        return stack[top + 1]


print(pop())

if top > -1:  # pop()
    top -= 1
    print(stack[top + 1])

 

Stack 연습 

 

stack = []
stack.append(1) # push(1)
stack.append(2) # push(2)
stack.append(3) # push(3)
print(stack.pop())
print(stack.pop())
print(stack.pop())

# 3
# 2
# 1

 

[연습 문제 1] TOP 을 이동하면서 push / pop 해보기

STACK_SIZE = 10
stack = [0] * STACK_SIZE
top = -1

top += 1    # push(1)
stack[top] = 1
top += 1    # push(2)
stack[top] = 2
top += 1    # push(3)
stack[top] = 3

top -= 1
print(stack[top+1])
print(stack[top])
top -= 1
print(stack[top])
top -= 1

 

---

 

스택의 응용 1

스택 구현 고려 사항

• 1차원 배열을 사용하여 구현할 경우 구현이 용이하다는 장점이 있지만
  스택의 크기를 변경하기가 어렵다는 단점이 있다.

 

• 이를 해결하기 위한 방법으로 저장소를 동적으로 할당하여 스택을 구현하는 방법이 있다
  동적 연결리스트를 이용하여 구현하는 방법을 의미한다.
  구현이 복잡하다는 단점이 있지만 메모리를 효율적으로 사용한다는 장점을 가진다.
  스택의 동적 구현은 생략한다.

 

스택의 응용1 : 괄호검사

• 괄호의 종류 : 대괄호 [] 중괄호 {} 소괄호 ()
• 조건
  • 1) 왼쪽 괄호의 개수와 오른쪽 괄호의 개수가 같아야 한다.
  • 2) 같은 괄호에서 왼쪽 괄호는 오른쪽 괄호보다 먼저 나와야 한다.
  • 3) 괄호 사이에는 포함 관계만 존재한다.
• 잘못된 괄호 사용의 예
  • (a(b)
  • a(b)b)
  • a{b(c[d]e}f)

 

스택을 이용한 괄호 검사

 

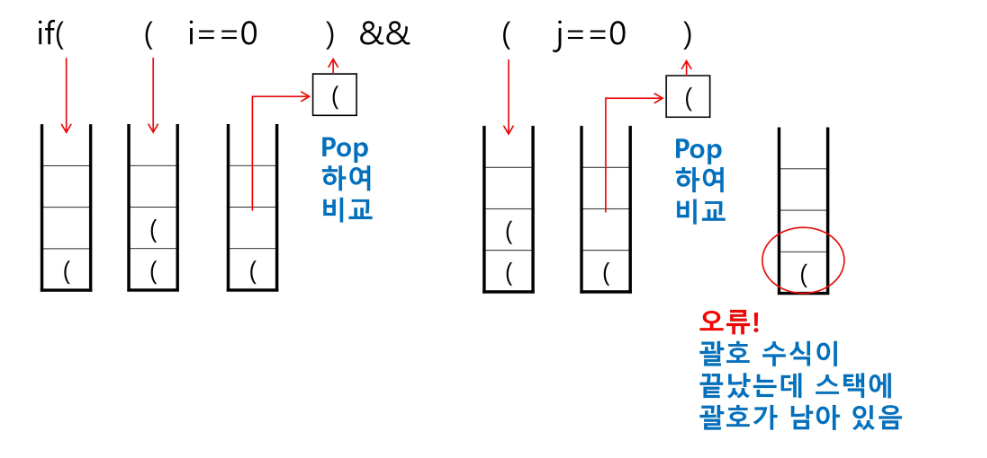
괄호를 조사하는 알고리즘 개요

• 문자열에 있는 괄호를 차례대로 조사하면서 왼쪽 괄호를 만나면 스택에 삽입하고,
  오른쪽 괄호를 만나면 스택에서 top 괄호를 삭제한 후 오른쪽 괄호와 짝이 맞는지를 검사한다.
• 이 때, 스택이 비어있으면 조건 1 또는 조건 2에 위배되고 괄호의 짝이 맞지 않으면 조건 3에 위배된다.
• 마지막 괄호까지를 조사한 후에도 스택에 괄호가 남아있으면 조건 1에 위배된다.

 

[연습문제 2] 괄호의 짝을 검사하는 프로그램을 작성해보자.

• 작성한 프로그램으로 다음 괄호 사용을 검사해보자.
  ()()((()))
  ((()((((()()((()())((())))))

 

def is_valid_parentheses(s):
    stack = []
    for char in s:
        if char == '(':
            stack.append(char)
        elif char == ')':
            if not stack:   # 스택이 비어있는데 닫는 괄호가 나온 경우
                return False
            stack.pop()

    return len(stack) == 0  # 스택이 비어있으면 True, 아니면 False

# 테스트
print(is_valid_parentheses('()()((()))'))
print(is_valid_parentheses('((()((((()()((()())((())))))'))

# True
# False

 

스택의 응용 2

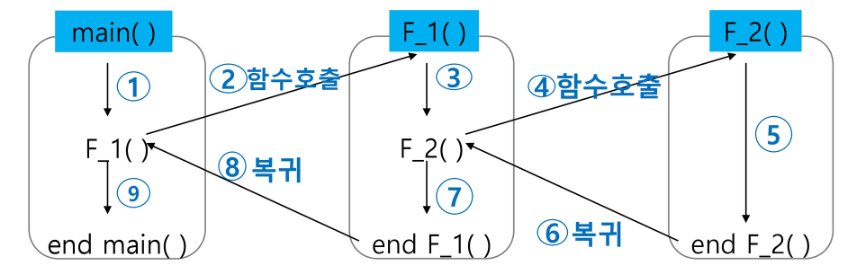
Function call

• 프로그램에서의 함수 호출과 복귀에 따른 수행 순서를 관리
  • 가장 마지막에 호출된 함수가 가장 먼저 실행을 완료하고 복귀하는 후입선출 구조이므로,
    후입선출 구조의 스택을 이용하여 수행순서 관리

 

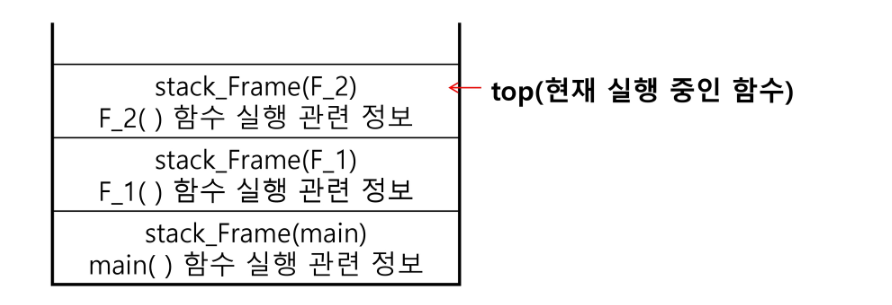
• 함수 호출이 발생하면 호출한 함수 수행에 필요한 지역변수, 매개변수 및 수행 후 복귀할 주소 등의 정보를
  스택 프레임(stack frame)에 저장하여 시스템 스택에 삽입

 

 

•  함수의 실행이 끝나면 시스템 스택의 top 원소 (스택 프레임)를 삭제 (pop) 하면서
  프레임에 저장되어 있던 복귀주소를 확인하고 복귀
• 함수 호출과 복귀에 따라 이 과정을 반복하여 전체 프로그램 수행이 종료되면 시스템 스택은 공백 스택이 된다.

 

---