재귀 호출

재귀호출

• 필요한 함수가 자신과 같은 경우 자신을 다시 호출하는 구조
• 함수에서 실행해야 하는 작업의 특성에 따라 일반적인 호출방식보다
  재귀호출방식을 사용하여 함수를 만들면 프로그램의 크기를 줄이고 간단하게 작성
  • 재귀 호출의 예) factorial

 

n에 대한 factorial : 1부터 n까지의 모든 자연수를 곱하여 구하는 연산

n! = n x (n-1)!
    (n-1)! = (n-1) x (n-2)!
    (n-2)! = (n-2) x (n-3)!

...
    2! = 2 x 1!
    1! = 1

 

마지막에 구한 하위 값을 이용하여 상위 값을 구하는 작업을 반복

 

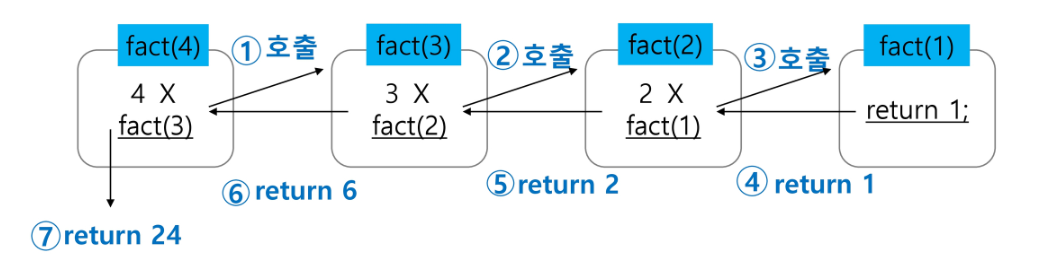
• factorial 함수에서 n=4 인 경우의 실행

 

피보나치 수열

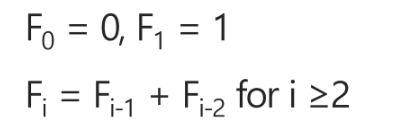
• 0과 1로 시작하고 이전의 두 수 합을 다음 항으로 하는 수열을 피보나치라 한다.
  • 0, 1, 1, 2, 3, 5, 8, 13, ...
• 피보나치 수열의 i번 째 값을 계산하는 함수 F를 정의하면 다음과같다.

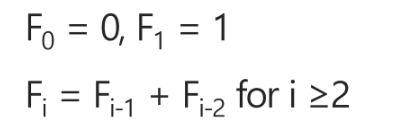
• 위의 정의로부터 피보나치 수열의 i번째 항을 반환하는 함수를 재귀함수로 구현할 수 있다.

 

피보나치 수를 구하는 재귀함수

def fibo(n):
    if n < 2:
        return n
    else:
        return fibo(n-1) + fibo(n-2)

 

---

 

재귀 호출 연습

• 모든 배열 원소에 접근하기

def f(i, N):    #크기 N인 배열 arr[i]에 접근
    if i == N:
        return
    else:
        print(arr[i])
        f(i+1, N)

def f(i, N, v): # v 찾는 값
    if i == N:
        return 0
    elif arr[i] == v:
        return 1
    else:
        reuturn f(i+1, N)

 

Memoization

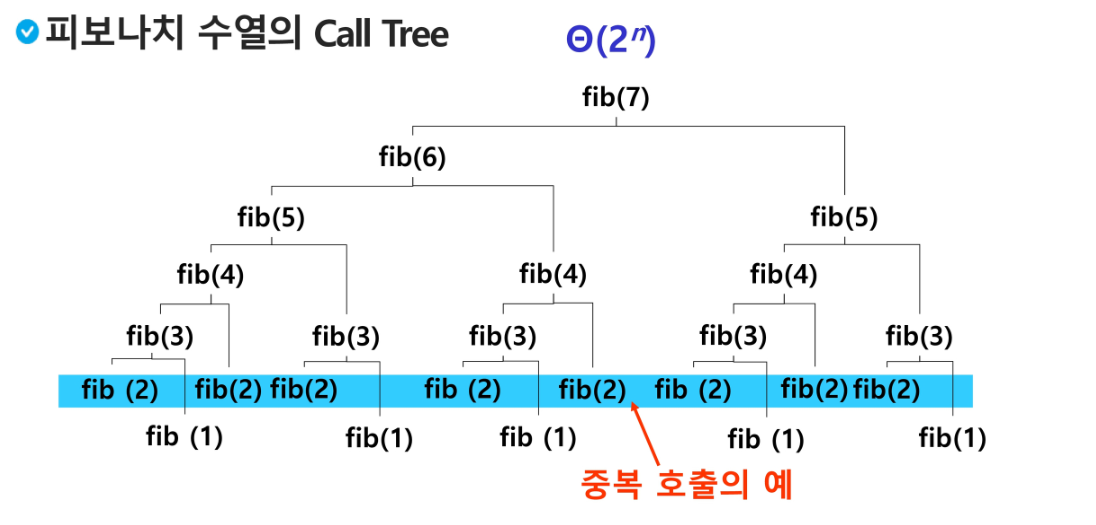
• 앞의 예에서 피보나치 수를 구하는 함수를 재귀함수로 구현한 알고리즘은 문제점이 있다.
• '엄청난 중복 호출이 존재한다' 는 것이다.

 

• 메모이제이션은 컴퓨터 프로그램을 실행할 때 이전에 계산한 값을 메모리에 저장해서 매번 다시 계산하지
  않도록 하여 전체적인 실행속도를 빠르게 하는 기술이다. 동적 계획법의 핵심이 되는 기술이다.
• 'memoization'은 글자 그대로 해석하면 '메모리에 넣기(to put in memory)' 라는 의미이며 '기억되어야 할 것'
  이라는 뜻의 라틴어에서 파생되었다.
• 앞의 예에서 피보나치 수를 구하는 알고리즘에서 fibo(n)의 값을 계산하자마자 저장하면 (memoize), 실행시간을 O(n) 으로 줄일 수 있다.

 

Memoization 방법을 적용한 알고리즘

def fibo1(n):
    global memo
    if n >= 2 and memo[n] == 0:
        memo[n] = fibo1(n - 1) + fibo1(n - 2)
    return memo[n]


memo = [0] * (n + 1)
memo[0] = 0
memo[1] = 1